Exercices corrigés : Probabilités

Fiche d'exercices N°1 - correction fiche d'exercices N°1. Fiche d'exercices N°2 - correction fiche d'exercices N°2. Fiche d'exercices N°3 - correction fiche d'exercices N°3. Fiche d'exercices N°4 - correction fiche d'exercices N°4. Fiche d'exercices N°5 - correction fiche d'exercices N°5. Fiche d'exercices N°6 - correction fiche d'exercices N°6. Fiche d'exercices N°7 - correction fiche d'exercices N°7. Fiche d'exercices N°8 - correction fiche d'exercices N°8. Fiche d'exercices N°9 - correction fiche d'exercices N°9. Fiche d'exercices N°10 - correction fiche d'exercices N°10.

Résumé de cours : Probabilités

Introduction

La probabilité mesure la chance qu'un événement se produise. Elle est toujours comprise entre 0 et 1 (ou entre 0% et 100%). Une probabilité de 0 signifie que l'événement est impossible, et une probabilité de 1 signifie qu'il est certain.

Définition

La probabilité d'un événement est le rapport entre le nombre de cas favorables et le nombre total de cas possibles.

\( P(E) = \frac{\text{nombre de cas favorables}}{\text{nombre total de cas possibles}} \)

Expérience aléatoire

Une expérience est dite aléatoire si on ne peut pas prévoir l'issue avant de la réaliser, mais si toutes ses issues possibles sont connues à l'avance.

Événements

Un événement est un ensemble d'issues d'une expérience aléatoire. Un événement est dit élémentaire s'il est constitué d'une seule issue.

Exemples

Lancer d'un dé

Si l'on lance un dé équilibré à 6 faces, la probabilité d'obtenir un 3 est \( \frac{1}{6} \) car il y a 1 cas favorable (obtenir un 3) sur 6 cas possibles (obtenir un 1, 2, 3, 4, 5 ou 6).

Tirer une carte d'un jeu de 52 cartes

La probabilité de tirer une dame est \( \frac{4}{52} \) ou \( \frac{1}{13} \) car il y a 4 dames dans un jeu de 52 cartes.

Propriétés des probabilités

• La probabilité d'un événement certain est 1.
• La probabilité d'un événement impossible est 0.
• La somme des probabilités de tous les événements élémentaires d'une expérience aléatoire est égale à 1.

Probabilité d'événements complémentaires

Si \( A \) est un événement, alors son événement complémentaire (noté \( \bar{A} \)) est l'événement "A ne se produit pas".

\( P(\bar{A}) = 1 - P(A) \)

Exemple

Si la probabilité qu'il pleuve demain est de 0,7, alors la probabilité qu'il ne pleuve pas est \( 1 - 0,7 = 0,3 \).

Tirage avec et sans remise

Lorsqu'on effectue des tirages successifs, la manière dont on procède après chaque tirage change la nature des probabilités associées.

Tirage avec remise

Dans un tirage avec remise, après avoir tiré un élément, on le remet dans l'ensemble initial avant d'effectuer le tirage suivant. Chaque tirage est donc indépendant des autres.

Exemple :

Si on tire une carte d'un jeu de 52, puis qu'on la remet avant de tirer une nouvelle carte, la probabilité de tirer une dame lors du premier tirage est \( \frac{4}{52} \) et la probabilité de tirer une dame lors du second tirage est toujours \( \frac{4}{52} \), car le jeu est toujours complet.

Tirage sans remise

Dans un tirage sans remise, une fois qu'un élément est tiré, il n'est pas remis dans l'ensemble initial. Les tirages successifs ne sont donc pas indépendants.

Exemple :

Si on tire une carte d'un jeu de 52 et qu'on ne la remet pas, la probabilité de tirer une dame lors du premier tirage est \( \frac{4}{52} \). Si cette première carte est une dame, la probabilité de tirer une dame lors du second tirage devient \( \frac{3}{51} \), car il ne reste que 3 dames parmi les 51 cartes restantes. Si la première carte n'était pas une dame, la probabilité serait alors \( \frac{4}{51} \) pour le second tirage.

Conclusion sur les tirages

La nature du tirage (avec ou sans remise) influence les probabilités associées aux tirages successifs. Il est essentiel de bien comprendre le type de tirage effectué pour déterminer correctement les probabilités associées.

Arbres de Probabilités

Les arbres de probabilités sont des outils visuels puissants pour représenter et calculer les probabilités conditionnelles et les résultats d'une série d'expériences aléatoires. Chaque branche de l'arbre représente un résultat possible avec sa probabilité associée.

Exemple d'Arbre de Probabilités :

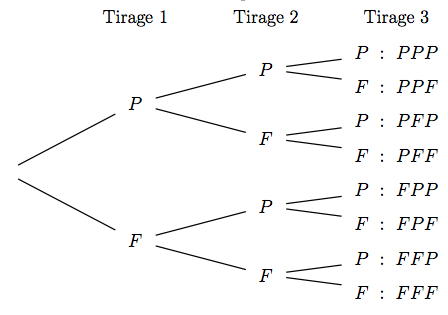
Dans cet exemple, nous pouvons voir un arbre de probabilités pour le lancer d'une pièce de monnaie. Il montre toutes les issues possibles (face ou pile) à chaque étape du lancer de la pièce. Les probabilités sont attribuées à chaque branche, ce qui permet de calculer la probabilité de chaque résultat.

Conclusion

Les probabilités permettent de mesurer mathématiquement le degré d'incertitude associé à des expériences aléatoires. Avec une bonne compréhension de cette notion, on peut prendre des décisions plus éclairées dans des situations d'incertitude.