Exercices corrigés : Décomposition des nombres décimaux

Fiche d'exercices N°1 - correction fiche d'exercices N°1. Fiche d'exercices N°2 - correction fiche d'exercices N°2. Fiche d'exercices N°3 - correction fiche d'exercices N°3. Fiche d'exercices N°4 - correction fiche d'exercices N°4. Fiche d'exercices N°5 - correction fiche d'exercices N°5. Fiche d'exercices N°6 - correction fiche d'exercices N°6. Fiche d'exercices N°7 - correction fiche d'exercices N°7. Fiche d'exercices N°8 - correction fiche d'exercices N°8.

Résumé de cours : Décomposition des nombres décimaux

Définition des nombres décimaux

Un nombre décimal est un nombre qui possède une partie entière et une partie décimale, séparées par une virgule. Par exemple :

• 15,47
• 3 217,019
• 0,0037

Décomposition en milliers, centaines, dizaines, unités, dixièmes, centièmes, millièmes

Pour décomposer un nombre décimal en milliers, centaines, dizaines, unités, dixièmes, centièmes et millièmes, on utilise les règles suivantes :

• Le chiffre situé à gauche de la virgule est le chiffre des unités.
• Le chiffre situé à la gauche du chiffre des unités est le chiffre des dizaines.
• Le chiffre situé à la gauche du chiffre des dizaines est le chiffre des centaines.
• Le chiffre situé à la gauche du chiffre des centaines est le chiffre des milliers.
• Le chiffre situé à la droite de la virgule est le chiffre des dixièmes.
• Le chiffre situé à deux positions à droite de la virgule est le chiffre des centièmes.
• Le chiffre situé à trois positions à droite de la virgule est le chiffre des millièmes.

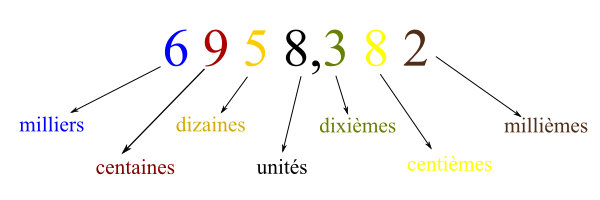
Par exemple :

• 15,47 = 1 x 10 + 5 x 1 + 4 x 1/10 + 7 x 1/100
• 3 217,019 = 3 x 1000 + 2 x 100 + 1 x 10 + 7 x 1 + 1 x /100 + 9 x 1/1000
• 0,037 =0 + 3 x 1/100 + 7 x 1/1000
• 3 215,625 = 3 x 1000 + 2 x 100 + 1 x 10 + 5 x 1 + 6 x 1/10 + 2 x 1/100 + 5 x 1/1000

Exemples

Voici 10 exemples à étudier pour mieux comprendre la décomposition d'un nombre décimal en milliers, centaines, dizaines, unités, dixièmes, centièmes et millièmes :

• 235,04 = 2 x 100 + 3 x 10 + 5 x 1 + 4 x 1/100


• 9,126 = 9 x 1 + 1 x 1/10 + 2 x 1/100 + 6 x 1/1000


• 17,909 = 1 x 10 + 7 x 1 + 9 x 1/10 + 9 x 1/1000


• 5 432,321 = 5 x 1000 + 4 x 100 + 3 x 10 + 2 x 1 + 3 x 1/10 + 2 x 1/100 + 1 x 1/1000


• 0,015 = 0 + 1 x 1/100 + 5 x 1/1000


• 678,055 = 6 x 100 + 7 x 10 + 8 x 1 + 5 x 1/100 + 5 x 1/1000


• 0,87 = 8 x 1/10 + 7 x 1/100


• 1 232,123 = 1 x 1000 + 2 x 100 + 3 x 10 + 2 x 1 + 1 x 1/10 + 2 x 1/100 + 3 x 1/1000


• 8,21 =8 x 1 + 2 x 1/10 + 1 x 1/100


• 4,009 = 4 x 1 + 9 x 1/1000

Autres points concernant la décomposition des nombres décimaux

• La décomposition d'un nombre décimal peut être utilisée pour effectuer des opérations arithmétiques telles que l'addition, la soustraction, la multiplication et la division.


• Lorsque l'on ajoute ou soustrait des nombres décimaux, il est important de bien aligner les chiffres des mêmes rangs décimaux pour faciliter la manipulation des nombres.


• Lorsque l'on multiplie ou divise des nombres décimaux, on peut souvent simplifier les calculs en déplaçant la virgule à la position appropriée avant de procéder aux opérations.


• Les nombres décimaux peuvent également être comparés en utilisant les symboles mathématiques >, < et = en fonction de leur valeur.


• Il est important de bien comprendre la place de la virgule dans un nombre décimal et comment elle affecte la décomposition et les opérations arithmétiques qui y sont liées.