Exercices corrigés : Aire de disque

Fiche d'exercices N°1 - correction fiche d'exercices N°1. Fiche d'exercices N°2 - correction fiche d'exercices N°2. Fiche d'exercices N°3 - correction fiche d'exercices N°3. Fiche d'exercices N°4 - correction fiche d'exercices N°4. Fiche d'exercices N°5 - correction fiche d'exercices N°5. Fiche d'exercices N°6 - correction fiche d'exercices N°6. Fiche d'exercices N°7 - correction fiche d'exercices N°7. Fiche d'exercices N°8 - correction fiche d'exercices N°8. Fiche d'exercices N°9 - correction fiche d'exercices N°9. Fiche d'exercices N°10 - correction fiche d'exercices N°10.

Résumé de cours : Aire de disque

Prérequis

Avant de commencer cette leçon, assurez-vous de comprendre les concepts de rayon, de diamètre d'un cercle, et du nombre \( \pi \) (pi).

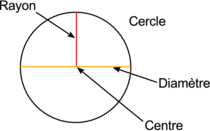
Le Nombre \( \pi \) (pi)

Le nombre (pi), souvent représenté par la lettre grecque \( \pi \), est une constante mathématique qui représente le rapport entre la circonférence d'un cercle et son diamètre. Il est approximativement égal à 3.14159, mais sa valeur exacte est en réalité irrationnelle, ce qui signifie qu'elle a une infinité de décimales sans répétition ni motif régulier.

Objectif et Attentes

À la fin de cette leçon, vous serez capable de:

• Identifier le rayon et le diamètre d'un cercle.
• Calculer l'aire de n'importe quel disque en utilisant la formule appropriée.

Compétences Développées

• Comprendre le concept d'aire d'un disque.
• Utiliser la formule pour calculer l'aire d'un disque.
• Appliquer la formule dans des situations pratiques.

Exemples

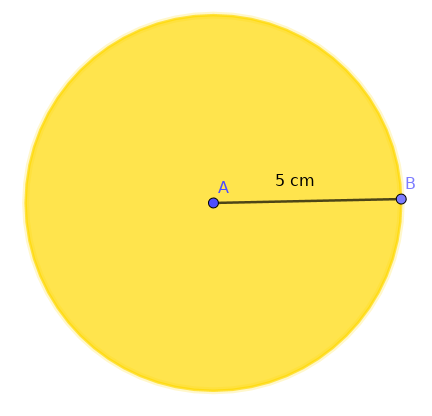
Si un disque a un rayon de 5 cm, son aire est donnée par la formule \( A = \pi r^2 \). Pour un rayon de 5 cm, cela donne \( A = \pi \times 5^2 = 78.54 \) cm² (en arrondissant à deux décimales).

Exercices

1. Calculez l'aire d'un disque avec un rayon de 3 cm.
2. Si le diamètre d'un disque est de 10 cm, quelle est son aire? (Astuce: le rayon est la moitié du diamètre)

Résumé

L'aire d'un disque est calculée en utilisant la formule \( A = \pi r^2 \), où \( r \) est le rayon du disque. C'est l'espace à l'intérieur du cercle.

Calcul de l'Aire Annulaire

L'aire annulaire est l'espace entre deux cercles : un grand cercle et un petit cercle inscrit à l'intérieur. Pour calculer l'aire annulaire, nous soustrayons l'aire du petit cercle de l'aire du grand cercle.

Formule de l'aire annulaire : \( A_{annulaire} = \pi R^2 - \pi r^2 \)

où \( R \) est le rayon du grand cercle et \( r \) est le rayon du petit cercle.

Exemple

Si un grand cercle a un rayon de 7 cm et un petit cercle inscrit a un rayon de 4 cm, l'aire annulaire est :

\( A_{annulaire} = \pi \times 7^2 - \pi \times 4^2 = 153.94 \) cm² (en arrondissant à deux décimales).

Exercices

1. Calculez l'aire annulaire entre un grand cercle de rayon 10 cm et un petit cercle de rayon 6 cm.
2. Si le rayon du grand cercle est de 8 cm et que l'aire annulaire est de 50.27 cm², quel est le rayon du petit cercle?

Conseils et Erreurs à Éviter

• Assurez-vous de toujours utiliser le rayon et non le diamètre dans la formule.
• Arrondissez votre réponse à deux décimales pour plus de précision.
• Ne confondez pas le rayon avec le diamètre. Le rayon est toujours la moitié du diamètre.