Exercices corrigés : Construction triangles

Fiche d'exercices N°1 - correction fiche d'exercices N°1. Fiche d'exercices N°2 - correction fiche d'exercices N°2. Fiche d'exercices N°3 - correction fiche d'exercices N°3. Fiche d'exercices N°4 - correction fiche d'exercices N°4. Fiche d'exercices N°5 - correction fiche d'exercices N°5. Fiche d'exercices N°6 - correction fiche d'exercices N°6. Fiche d'exercices N°7 - correction fiche d'exercices N°7. Fiche d'exercices N°8 - correction fiche d'exercices N°8. Fiche d'exercices N°9 - correction fiche d'exercices N°9. Fiche d'exercices N°10 - correction fiche d'exercices N°10.

Résumé de cours : Construction triangles

Introduction

Les triangles, ces figures à trois côtés, sont partout autour de nous et sont la base de nombreuses constructions en mathématiques. Mais tous les triangles ne sont pas créés de la même manière. Plongeons-nous dans le monde fascinant des triangles!

Prérequis

Avant de plonger dans les profondeurs des triangles, assurez-vous de connaître les bases des figures géométriques et de savoir comment mesurer les angles.

Objectif et Attentes

À la fin de cette leçon, non seulement vous serez capable d'identifier différents types de triangles, mais vous comprendrez aussi pourquoi ils sont si importants et comment ils sont utilisés dans le monde réel.

Compétences Développées

• Identification des différents types de triangles.
• Compréhension des propriétés uniques de chaque triangle.
• Application des connaissances des triangles dans des situations pratiques.

Rappels sur les Prérequis

Un triangle est formé lorsque trois droites non parallèles se croisent. Les points où ils se croisent sont appelés sommets. Les segments entre les sommets sont les côtés du triangle.

Définition et Propriétés

Triangle Rectangle

C'est un triangle qui a un angle de 90°. Imaginez que vous êtes debout et que votre ombre forme un angle droit avec le sol. C'est un exemple de triangle rectangle!

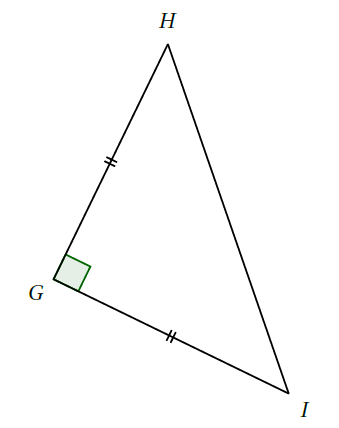
Triangle Équilatéral

Imaginez un triangle parfait où tous les côtés et tous les angles sont exactement identiques. C'est un triangle équilatéral!

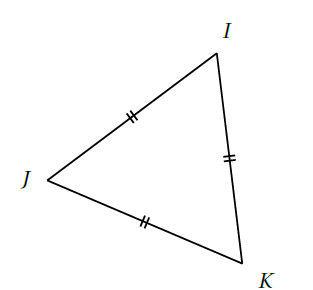
Triangle Isocèle

Un triangle qui a deux côtés de même longueur. C'est comme avoir deux bras de la même longueur!

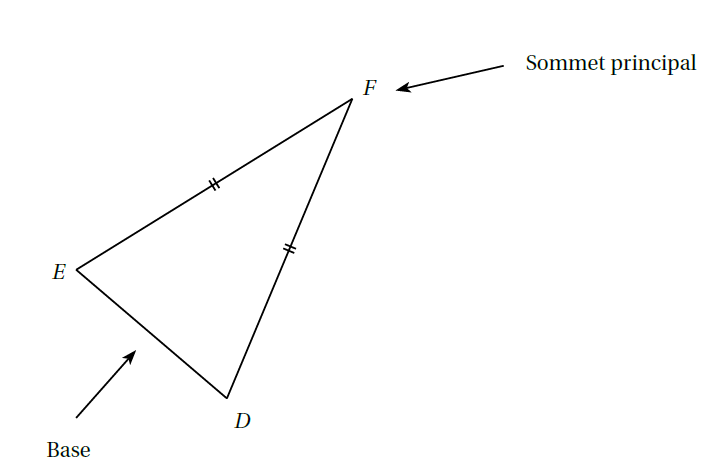
Exemples et Exercices

Exemple 1

Si vous avez un triangle rectangle ABC avec AB = 3 cm et AC = 4 cm, pouvez-vous utiliser le théorème de Pythagore pour trouver la longueur de BC?

Exercice 1

Dessinez un triangle isocèle et indiquez ses propriétés. Comment pouvez-vous prouver qu'il s'agit bien d'un triangle isocèle?

Correction

Un triangle isocèle a deux côtés de même longueur. Si vous mesurez les côtés et qu'ils sont égaux, alors c'est un triangle isocèle!

Applications Pratiques

Les triangles sont la base de nombreuses structures, des pyramides d'Égypte aux toits de nos maisons. Ils sont solides, stables et esthétiquement plaisants.

Résumé

Les triangles sont plus que de simples figures à trois côtés. Ils ont des propriétés uniques qui les rendent essentiels dans de nombreux domaines, de l'art à l'ingénierie.

Conseils et Erreurs à Éviter

• Ne présumez pas du type de triangle basé uniquement sur son apparence. Mesurez toujours!
• Ne confondez pas un angle aigu avec un angle droit.
• Pratiquez, pratiquez, pratiquez! Plus vous travaillez avec des triangles, mieux vous les comprendrez.