CLASSE DE 5ème
Exercices corrigés : Symétrie centrale
Résumé de cours : Symétrie axiale et centrale
Introduction
La symétrie est partout autour de nous, dans la nature, l'art, l'architecture et bien sûr, les mathématiques. Comprendre la symétrie, c'est apprendre à voir le monde d'une manière structurée et ordonnée.
Prérequis
Connaissance des figures géométriques de base, capacité à tracer des droites et des points sur une feuille.
Objectif et Attentes
À la fin de cette leçon, vous serez capable de:
- Identifier différents types de symétries.
- Appliquer la symétrie centrale pour transformer des figures.
- Reconnaître la symétrie dans le monde qui vous entoure.
Compétences Développées
- Reconnaissance et tracé d'axes de symétrie.
- Transformation de figures utilisant la symétrie centrale.
- Application de la symétrie dans des situations réelles.
Rappels sur les Prérequis
La symétrie est une transformation qui permet de superposer une figure à son image. Si vous pliez une figure symétrique en deux le long de son axe de symétrie, les deux moitiés coïncideront parfaitement.
Types de Symétrie
Symétrie Axiale
C'est la symétrie que la plupart des gens connaissent. Une figure est symétrique par rapport à une droite (l'axe de symétrie) si, en pliant le papier le long de cette droite, la figure se superpose à elle-même.
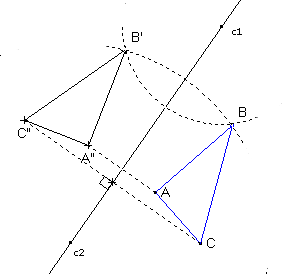
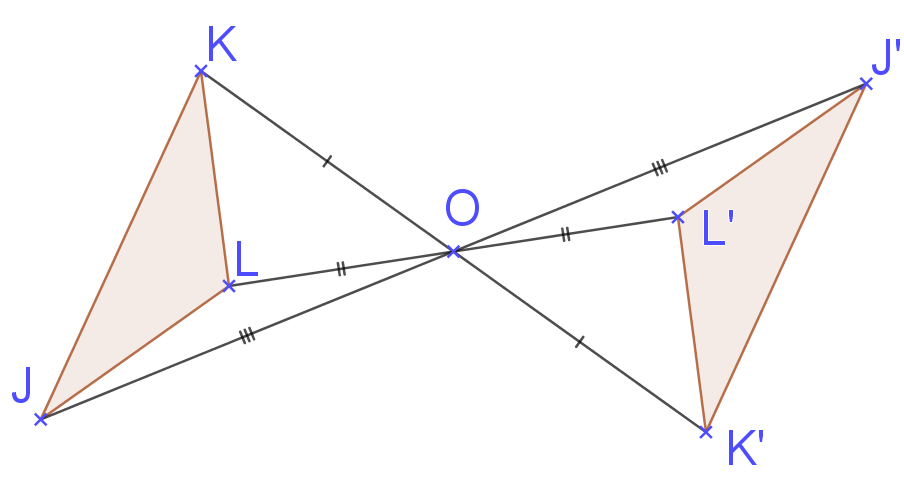
Symétrie Centrale
Une figure a une symétrie centrale autour d'un point si, pour chaque point de la figure, le point diamétralement opposé par rapport au centre est aussi dans la figure.
Exemples et Exercices
Exemple 1
Un rectangle a deux axes de symétrie, chacun passant par le milieu de deux côtés opposés. Essayez de dessiner un rectangle et tracez ses axes de symétrie.
Exercice 1
Tracez tous les axes de symétrie d'un triangle équilatéral.
Correction
Un triangle équilatéral a trois axes de symétrie, chacun passant par un sommet et le milieu du côté opposé.
Applications Pratiques
La symétrie est omniprésente dans notre quotidien. Des motifs sur les carrelages, aux designs des bâtiments, en passant par les motifs sur les vêtements. La symétrie est également essentielle dans de nombreuses branches des mathématiques et des sciences.
Résumé
La symétrie est une propriété fondamentale qui permet de superposer une figure à son image. Elle peut être axiale ou centrale et est omniprésente dans le monde qui nous entoure.
Conseils et Erreurs à Éviter
- Toujours vérifier si une figure est symétrique par rapport à un axe ou un point donné.
- Ne pas confondre l'axe de symétrie avec le centre de symétrie.
- Pratiquez régulièrement pour améliorer votre capacité à reconnaître et dessiner des symétries.
Copyright © 2006 - Toupty.com
Tous droits réservés - Mentions légales
Plan du site
Contenu
Description


