Exercices corrigés : Symétrie et quadrillage

Fiche d'exercices N°1 - correction fiche d'exercices N°1. Fiche d'exercices N°2 - correction fiche d'exercices N°2. Fiche d'exercices N°3 - correction fiche d'exercices N°3. Fiche d'exercices N°4 - correction fiche d'exercices N°4. Fiche d'exercices N°5 - correction fiche d'exercices N°5. Fiche d'exercices N°6 - correction fiche d'exercices N°6. Fiche d'exercices N°7 - correction fiche d'exercices N°7. Fiche d'exercices N°8 - correction fiche d'exercices N°8.

Résumé de cours : Symétrie et quadrillage

Figure symétrique : définition

Deux figures sont dites symétriques si elles ont la même forme et la même taille, mais sont orientées de manière opposée. En d'autres termes, une figure symétrique est l'image miroir d'une autre figure. La symétrie peut être de deux types : la symétrie centrale et la symétrie axiale.

Symétrie centrale

La symétrie centrale est une transformation géométrique qui fait correspondre chaque point d'une figure à un autre point situé à la même distance du centre de symétrie, mais dans la direction opposée. Le centre de symétrie est le point équidistant de tous les points correspondants de la figure et de son image symétrique.

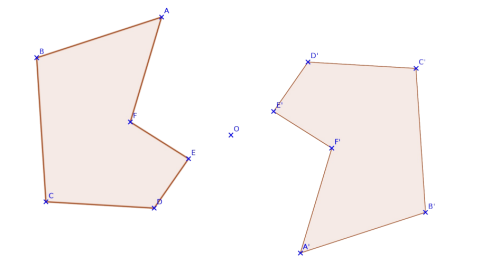
Exemple : un rectangle possède un centre de symétrie situé au point d'intersection de ses diagonales. Si vous pliez un rectangle en deux le long de ses diagonales, les deux moitiés coïncideront parfaitement, illustrant ainsi la symétrie centrale.

Symétrie axiale

La symétrie axiale, également appelée symétrie de réflexion, est une transformation géométrique qui fait correspondre chaque point d'une figure à un autre point situé à la même distance de l'axe de symétrie, mais de l'autre côté de cet axe. L'axe de symétrie est une droite qui divise la figure en deux parties égales et opposées (voir figure ci-dessous).

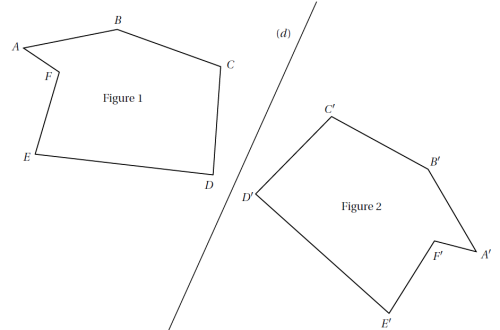
Exemple : un triangle isocèle possède un axe de symétrie qui passe par son sommet et qui est perpendiculaire à sa base. Si vous pliez un triangle isocèle le long de cet axe, les deux moitiés coïncideront parfaitement, illustrant ainsi la symétrie axiale.

Axe de symétrie

Un axe de symétrie est une droite qui divise une figure en deux parties égales et opposées. Si une figure est pliée le long de son axe de symétrie, les deux parties coïncideront parfaitement. Une figure peut avoir plusieurs axes de symétrie, un seul, ou aucun.

Exemples :

• Un carré possède quatre axes de symétrie : deux diagonales et deux médiatrices perpendiculaires à ses côtés.
• Un rectangle possède deux axes de symétrie : les médiatrices perpendiculaires à ses côtés.
• Un triangle équilatéral possède trois axes de symétrie : les médianes qui passent par chaque sommet et le milieu du côté opposé.
• Un triangle isocèle possède un axe de symétrie : la médiane qui passe par le sommet opposé à la base et qui est perpendiculaire à celle-ci.
• Un triangle quelconque (scalène) n'a pas d'axe de symétrie.
• Un cercle possède une infinité d'axes de symétrie : toutes les droites passant par son centre.

La symétrie est une propriété géométrique qui permet de comprendre et d'analyser la structure des figures. La symétrie centrale et la symétrie axiale sont deux types de transformations qui permettent de déterminer si une figure est symétrique ou non. L'étude des axes de symétrie aide à identifier les caractéristiques spécifiques des différentes figures géométriques.