CLASSE DE 5^ème

Exercices corrigés : Egalité de fractions

Fiche d'exercices N°1 - correction fiche d'exercices N°1. Fiche d'exercices N°2 - correction fiche d'exercices N°2. Fiche d'exercices N°3 - correction fiche d'exercices N°3. Fiche d'exercices N°4 - correction fiche d'exercices N°4. Fiche d'exercices N°5 - correction fiche d'exercices N°5. Fiche d'exercices N°6 - correction fiche d'exercices N°6. Fiche d'exercices N°7 - correction fiche d'exercices N°7. Fiche d'exercices N°8 - correction fiche d'exercices N°8. Fiche d'exercices N°9 - correction fiche d'exercices N°9. Fiche d'exercices N°10 - correction fiche d'exercices N°10.

Résumé de cours : Egalité de fractions

Introduction

Les fractions peuvent sembler compliquées, mais elles sont en réalité une manière simple et élégante de représenter des nombres. Imaginez partager une pizza ou diviser un gâteau, c'est là que les fractions entrent en jeu!

Prérequis

Avant de commencer, assurez-vous de connaître les nombres entiers et de comprendre la division.

Objectif et Attentes

À la fin de cette leçon, non seulement vous serez capable de travailler avec des fractions, mais vous comprendrez aussi comment elles fonctionnent et pourquoi elles sont si utiles.

Compétences Développées

• Comprendre la structure des fractions.
• Déterminer l'égalité entre deux fractions.
• Appliquer les fractions dans des situations concrètes.

Rappels sur les Prérequis

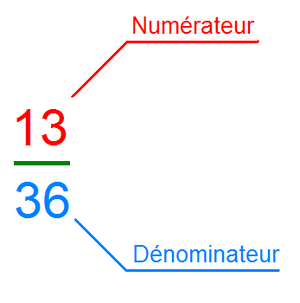
Une fraction est composée de deux parties: le numérateur (le nombre du haut) qui représente la partie que nous considérons, et le dénominateur (le nombre du bas) qui représente le tout.

Définition et Propriétés

Une fraction est une manière de représenter une division non effectuée. Pour savoir si deux fractions sont égales, on peut les simplifier ou les mettre au même dénominateur et comparer les numérateurs.

Simplification des Fractions

La simplification d'une fraction consiste à la réduire à sa forme la plus simple tout en conservant sa valeur. Pour simplifier une fraction, on divise le numérateur et le dénominateur par leur plus grand commun diviseur (PGCD).

Exemple de Simplification

Considérons la fraction \( \frac{8}{12} \). Le PGCD de 8 et 12 est 4. Si nous divisons le numérateur et le dénominateur par 4, nous obtenons:

\[ \frac{8 \div 4}{12 \div 4} = \frac{2}{3} \]

Donc, \( \frac{8}{12} \) simplifié donne \( \frac{2}{3} \).

Réduction au Même Dénominateur

Pour comparer, additionner ou soustraire des fractions, il est souvent nécessaire de les avoir avec le même dénominateur. Pour ce faire, on cherche le plus petit commun multiple (PPCM) des dénominateurs et on ajuste les fractions en conséquence.

Exemple de Réduction au Même Dénominateur

Considérons les fractions \( \frac{3}{4} \) et \( \frac{5}{6} \). Le PPCM de 4 et 6 est 12. Pour avoir le même dénominateur:

\[ \frac{3}{4} = \frac{3 \times 3}{4 \times 3} = \frac{9}{12} \] \[ \frac{5}{6} = \frac{5 \times 2}{6 \times 2} = \frac{10}{12} \]

Les deux fractions avec le même dénominateur sont \( \frac{9}{12} \) et \( \frac{10}{12} \).

Exemples et Exercices

Exemple 1

Si nous avons deux fractions, \( \frac{2}{4} \) et \( \frac{1}{2} \), comment savoir si elles sont égales?

En simplifiant \( \frac{2}{4} \), nous obtenons \( \frac{1}{2} \). Ainsi, les deux fractions sont égales!

Exercice 1

Les fractions \( \frac{3}{6} \) et \( \frac{2}{4} \) sont-elles égales? Essayez de les simplifier pour trouver la réponse.

Correction

En simplifiant \( \frac{3}{6} \) et \( \frac{2}{4} \), nous obtenons toutes deux \( \frac{1}{2} \). Donc, les deux fractions sont égales!

Applications Pratiques

Imaginez diviser une barre de chocolat entre amis ou mesurer des ingrédients pour une recette. Les fractions sont partout dans notre vie quotidienne!

Résumé

Les fractions sont essentielles en mathématiques et dans la vie quotidienne. Elles nous permettent de représenter des nombres qui ne sont pas entiers et de travailler avec eux.

Conseils et Erreurs à Éviter

• Ne présumez pas de l'égalité de deux fractions basée uniquement sur leur apparence. Simplifiez-les toujours!
• Ne confondez pas le numérateur avec le dénominateur.
• Pratiquez régulièrement pour renforcer votre compréhension.