Exercices corrigés : Aire et quadrillage

Fiche d'exercices N°1 - correction fiche d'exercices N°1. Fiche d'exercices N°2 - correction fiche d'exercices N°2. Fiche d'exercices N°3 - correction fiche d'exercices N°3. Fiche d'exercices N°4 - correction fiche d'exercices N°4. Fiche d'exercices N°5 - correction fiche d'exercices N°5. Fiche d'exercices N°6 - correction fiche d'exercices N°6. Fiche d'exercices N°7 - correction fiche d'exercices N°7. Fiche d'exercices N°8 - correction fiche d'exercices N°8.

Résumé de cours : Aire et quadrillage

Aire et quadrillage

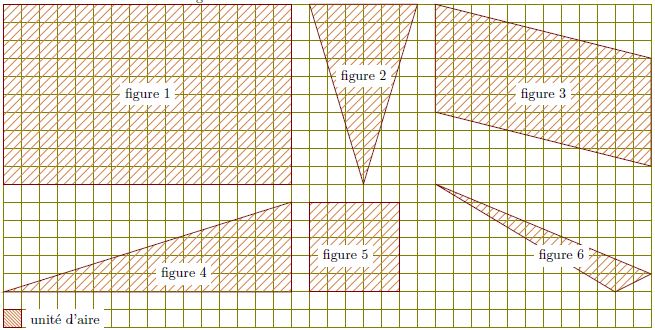
L'aire est une mesure de la surface d'une figure géométrique en deux dimensions. Pour calculer l'aire d'une figure, on peut utiliser le quadrillage, qui consiste à diviser la figure en unités de surface (généralement des carrés de même taille) et à compter le nombre d'unités qui la composent. Cela peut être particulièrement utile pour les figures géométriques complexes ou irrégulières.

Exemple : pour calculer l'aire d'un rectangle, on peut diviser sa surface en carrés de 1 cm de côté, puis compter le nombre total de carrés.

Aire d'un triangle

Pour calculer l'aire d'un triangle, on utilise la formule suivante :

Aire = (base × hauteur) / 2

La base et la hauteur doivent être perpendiculaires l'une à l'autre. Cette formule fonctionne pour tous les types de triangles (équilatéral, isocèle et scalène).

Exemple : un triangle a une base de 6 cm et une hauteur de 4 cm. Son aire est de (6 × 4) / 2 = 12 cm².

Aire d'un disque

Pour calculer l'aire d'un disque, on utilise la formule suivante :

Aire = π × rayon²

Le symbole "π" (pi) est une constante mathématique dont la valeur est d'environ 3,14. Le rayon est la distance entre le centre du disque et n'importe quel point sur sa circonférence.

Exemple : un disque a un rayon de 5 cm. Son aire est de π × 5² = 3,14 × 25 ? 78,5 cm².

Périmètre

Le périmètre est la mesure de la longueur totale des côtés d'une figure géométrique en deux dimensions. Pour calculer le périmètre d'une figure, il suffit d'additionner les longueurs de tous ses côtés.

Exemple : un rectangle a des côtés de 8 cm et 5 cm. Son périmètre est de (2 × 8) + (2 × 5) = 26 cm.

Autre exemple : un triangle équilatéral a des côtés de 6 cm. Son périmètre est de 3 × 6 = 18 cm.

Unités d'aire

Les unités d'aire sont utilisées pour exprimer la mesure de la surface d'une figure géométrique. Les unités d'aire les plus courantes sont les unités de surface métriques, telles que le centimètre carré (cm²), le mètre carré (m²) et le kilomètre carré (km²). Voici quelques conversions entre ces unités :

• 1 m² = 10 000 cm²
• 1 km² = 1 000 000 m²

D'autres unités d'aire incluent l'acre et l'hectare, qui sont couramment utilisées pour mesurer la surface de terrains.

• 1 hectare = 10 000 m²
• 1 acre ? 4 047 m²

Pour résumer, l'aire et le périmètre sont des mesures importantes en géométrie pour décrire la taille et la forme des figures en deux dimensions. Le quadrillage, les formules spécifiques pour les triangles et les disques, ainsi que la compréhension des unités d'aire, sont essentiels pour calculer l'aire et le périmètre de diverses figures géométriques.